[next] [prev] [prev-tail] [tail] [up]

A POV-Ray Usage Specifics

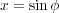
The raytracing program POV-Ray[2, 3] was used for the examples.

A.1 Sun Placement

The sun was set at a 3 degree horizontal and a 20 degree vertical angle from the origin by using the commands specified in figure 8.

light_source {  
   100000 * <-0.052336, 0.341551, -0.938405>  
   color rgb <1.0, 1.0, 1.0>  
   looks_like {  
      sphere {  
         100000 * <-0.052336, 0.341551, -0.938405>, 2000  
         pigment {  
            color rgb <1.0, 1.0, 1.0>  
         }  
         finish {  
            ambient 1.0  
         }  
      }  
   }  
}


Figure 8: POV-Ray Sun Placement Commands

To calculate the unit vector 〈-0.052336,0.341551,-0.938405〉 shown in figure 8, we let θ represent the vertical angle and we let φ represent the horizontal angle.

From this, the following formulas represent the unit vectors used:

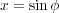x = sinφ
(1)

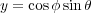y = cosφ sinθ
(2)

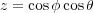z = cosφ cos θ
(3)

Verification that 〈x,y,z〉 is a unit vector can be accomplished with the formula

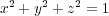x2 + y2 + z2 = 1
(4)

Using formulas 1, 2 and 3, as well as the relationship

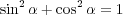sin2 α+ cos2α = 1
(5)

the following computations are performed:

x2 + y2 + z2 = (sinφ)2 + (cosφsin θ)2 + (cosφ cosθ)2 = sinφ2 sinφ + cosφsin θcosφsinθ+ cosφ cos θcosφcosθ = sin φ + cosφ sin θcosφsin θ+ cosφcosθ cosφ cosθ = sin2φ + cosφ cosφsinθsin θ+ cosφcosφ cosθcosθ = sin2φ + cos2φ sinθ sinθ + cosφ cosφcosθcosθ 2 2 2 = sin2φ + cos2φ sin2θ + cosφ2 cosφcosθcosθ = sin φ + cos φ sin θ + cos φ cosθcosθ = sin2φ + cos2φ sin2θ + cos2φ cos2θ = sin2φ + cos2φ(sin2 θ+ cos2θ) 2 2 = sin2φ + cos2φ(1) = sin φ + cos φ = 1 (6)

(Note: the hard-coding of the unit vector in figure 8 must be changed in time.)

There are extra commands available in case an area light is desired, as documented in §A.2.

A.2 Area Light Computations

If soft shadows from objects distant from, say, the ground are desired, this effect is simulated with an area light. This simulates the necessary umbra and penumbra in a manner much like the sun.

There is a plane the area lights are attached to, so to speak. To determine which way and which length the axis vectors u and v with a distance d are drawn are computed with the formulas

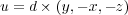u = d × (y,- x,- z)
(7)

and

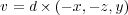v = d ×(- x,- z,y)
(8)

The commands used to do this are shown in figure 9.

   area_light  
   20000 * x, <0, 14142.1, 14142.1>, 15, 15  
   adaptive 4  
   circular


Figure 9: Extra Area Light Commands

In time, more accurate vector computation routines will be determined and used.

A.3 The Final Result

A picture showing a view of the “sun” approximating normal human visual angles is shown in figure 10.

PIC


Figure 10: View Of the Sun

This graphic is provided to check the placement and proportions of the sun. Code which generates this graphic is provided in figure 11.

camera {  
   location <-0.5, 1.8, 8>  
   look_at 100000 * <-0.052336, 0.258464, -0.964602>  
   up y  
   right 1.5*x  
}


Figure 11: Code For View Of the Sun

[next] [prev] [prev-tail] [front] [up]