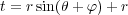
Out of sheer boredom, I provided the Perl script used to make the diagram seen in figure A.6. It is seen in figure E.1.
The key to making the diagram work is to remember that I am representing a circle in what is called an orthographic projection. I use the basic formulas
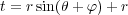 | (E.1) |
and
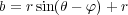 | (E.2) |
where r is the radius of the shape, such that it is drawn with a length of 2r, t is the position of the top of the line, b is the position of the bottom of the line, θ is the angle which the door is centered on, and φ is the angular size of the door. From that, the expression t - b is the length of the two vertical lines for each door.